When My Math Class Mastered One Thing
They show off in front of me!
While I and my Math Class were set to start “Completing of the Square”, on the MathLab No. 4 (a math class developed portfolio and style of our own of organizing quizzes, homework, and classwork with scores on them, which is an easy way of Math life at work!!!). An unusual class schedule before lunchtime, this quadratic equation topic has another beautiful method of solving the values of x. The class as usual equipped with a smartboard where students can vividly see the whole wide board top to bottom. As usual, I expect that my content shall bring them peace and harmony, but it was the opposite, chaos and violent reactions with new sets of solutions presented, here it all went…

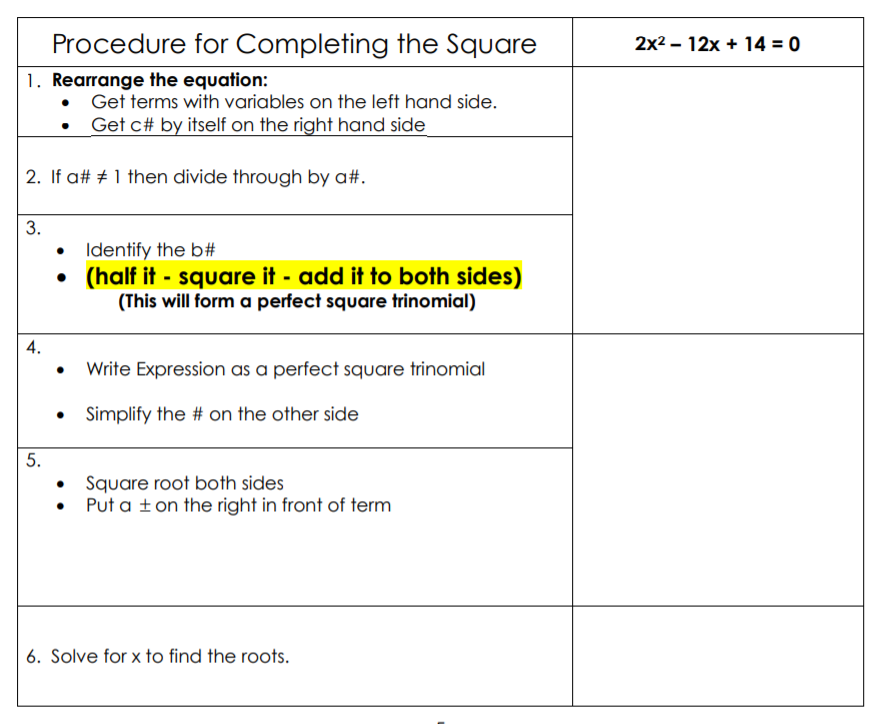
8th August 2020: Task Today: The 3rd Method We Use: Completing the Square: (written on the side of the smartboard screen: WE FINISHED: FACTORIZATION AND USING THE QUADRATIC FORMULA).
I showed them upfront the screen with 4 problems to solve. In no time, one student came up with his MathLab portfolio the 4-problems had been written down, solutions indicated and highlighted the answers! I was so amazed how in no time, didn’t struggle to solve whereas his classmates are also struggling to ask, praying to show solutions, etc.
So, I had to keep doing my routine to let the general class with the ordeal of not having understood the method earlier discussed. Almost all voices screaming out so loud, TEACHER, why you teach us so difficult, while other students already had 3 lines of solutions then done! Why not follow the student’s steps? easy and not long! Why don’t you put only the zero on the right!
I kept showing how completing the square and had an authoritative tone of bringing them to attention and had to listen but had violent reactions on how difficult the solution can be to bear on:
2x2+ 3x – 5 = 4
2x2+ 3x = 9
2x2 /2 + 3x/2 = 9/2
x2 + 3x/2 + [3/2 *1/2]2=9/2 + [3/4]2
x2 + 3x/2+ [3/4]2 = 9/2 + 9/16
[x + 3/4]2 = (72+9)/16
x + 3/4 = 
x + 3/4 = +9/4 – (1)
x + 3/4 = – 9/4 – (2)
From (1)
x = 9/4 -3/4
x = 6/4 = 3/2
Source: ALGEBRA UNIT 10-SOLVING QUADRATIC EQUATIONS
From (2),
x = (-3 – 9)/4
X = -12/4
x = – 3
Gave the student the floor to explain his work and wrote exactly the 2nd problem task and solved for 2 values of 2x2+ 3x – 5 = 4
Showed and so clearly and boldly written format: One student output explains:
2x2+ 3x – 5 – 4 = 0 e. g,. 2x2+ 3x – 9 = 0
: (2x-3) (x+3) = 0
: 2x – 3 = 0 ;
X = 3/2
x = -3
You see teacher? same same same!

As a classroom authority, I was a bit upset, why they had no time to listen to completing the square but had so much fun doing the FACTORIZATION! The lesson did for many weeks ago!
All students gone for lunch with an ordeal that COMPLETING the square had a terrible and long method and very difficult, and they had to brand me “KANIT YAK MAK”!
Looking at the bright side, I just realized that my Math Class had mastered one easy thing, something that they are proud of and something that they already love to use to solve similar problems involving quadratic equations. They have no time to listen to any other methods longer than ever imagined!


